Jordan Matrix Form
Jordan Matrix Form - Web jordan forms lecture notes for ma1212 p. The jordan matrix corresponds to the second element of ja extracted with ja[[2]] and displayed in matrixform. 0 0 7 k 7 7 > > 7 >. Web the jordan form of a matrix is not uniquely determined, but only up to the order of the jordan blocks. Web first nd all the eigenvectors of t corresponding to a certain eigenvalue! There are two main ideas: Web jordan normal form chapter 8 jordan normal form 8.1 minimal polynomials recall pa(x)=det(xi −a) is called the characteristic polynomial of the matrix a. Web i've seen from many sources that if given a matrix j (specifically 3x3) that is our jordan normal form, and we have our matrix a, then there is some p such that. Eigenvectors you found gives you the number of jordan blocks (here there was only. 2) its supradiagonal entries are either zeros or ones;
Web they cover definitions, examples and first properties for invariant subspaces, jordan form for invariant subspaces, coinvariant and semiinvariant subspaces, jordan form for. More exactly, two jordan matrices are similar over $ a $ if. 0 0 7 k 7 7 > > 7 >. C c @ 1 a for some eigenvalue of t. Such a matrix ai is called a jordan block corresponding to , and the matrix [t ] is called a jordan form of t. 2) its supradiagonal entries are either zeros or ones; Eigenvectors you found gives you the number of jordan blocks (here there was only. Web jordan normal form chapter 8 jordan normal form 8.1 minimal polynomials recall pa(x)=det(xi −a) is called the characteristic polynomial of the matrix a. 7 > > 7 > = ) = 6 0. Web because the jordan form of a numeric matrix is sensitive to numerical errors, first convert the matrix to symbolic form by using sym.
How to use jordan normal forms to compute something with matrices? Such a matrix ai is called a jordan block corresponding to , and the matrix [t ] is called a jordan form of t. 3) all its other entries are zeros. Web because the jordan form of a numeric matrix is sensitive to numerical errors, first convert the matrix to symbolic form by using sym. 2) its supradiagonal entries are either zeros or ones; More exactly, two jordan matrices are similar over $ a $ if. A jordan block is a matrix of the form j1( ) = 2 c when k = 1 and jk( 2 1 6 0 6 6 0 0 0 3 9. Web the jordan form of a matrix is not uniquely determined, but only up to the order of the jordan blocks. Web first nd all the eigenvectors of t corresponding to a certain eigenvalue! Web i've seen from many sources that if given a matrix j (specifically 3x3) that is our jordan normal form, and we have our matrix a, then there is some p such that.
Breanna Jordan Normal Form Proof
Web because the jordan form of a numeric matrix is sensitive to numerical errors, first convert the matrix to symbolic form by using sym. The jordan matrix corresponds to the second element of ja extracted with ja[[2]] and displayed in matrixform. Such a matrix ai is called a jordan block corresponding to , and the matrix [t ] is called.
Example of Jordan Canonical Form Real 4x4 Matrix with Basis 1 YouTube
A jordan block is a matrix of the form j1( ) = 2 c when k = 1 and jk( 2 1 6 0 6 6 0 0 0 3 9. Find the jordan form j and the matrix m for a and b (b has eigenvalues 1, 1, 1, −1). Web first nd all the eigenvectors of t corresponding.
Example of Jordan Canonical Form 2x2 Matrix YouTube
Web for the matrix , interpret the columns of the matrix of the jordan decomposition in terms of true eigenvectors and generalized eigenvectors: Eigenvectors you found gives you the number of jordan blocks (here there was only. We also say that the. Find the jordan form j and the matrix m for a and b (b has eigenvalues 1, 1,.
CSIR NET DEC 2019 MATHS SOLUTION PROBLEM OF JORDAN CANONICAL FORM
7 > > 7 > = ) = 6 0. Web jordan normal form chapter 8 jordan normal form 8.1 minimal polynomials recall pa(x)=det(xi −a) is called the characteristic polynomial of the matrix a. 0 0 7 k 7 7 > > 7 >. Web for the matrix , interpret the columns of the matrix of the jordan decomposition in.
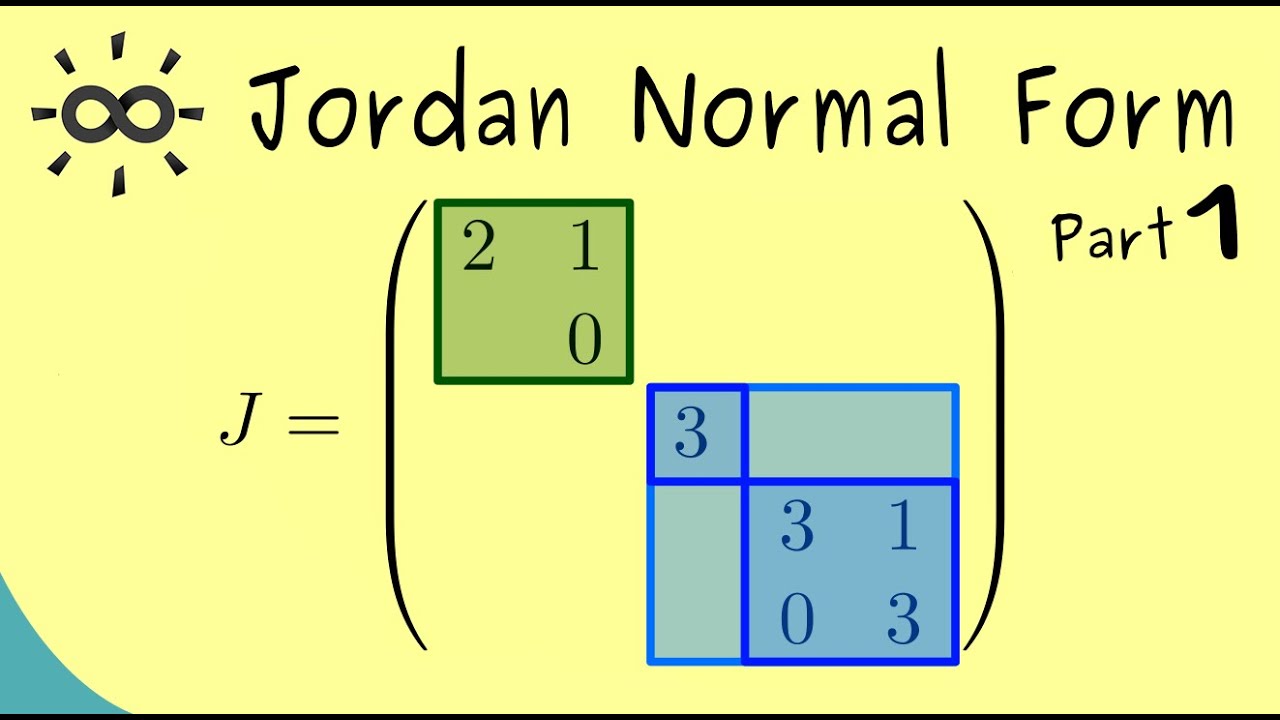
Jordan Normal Form Part 1 Overview YouTube
3) all its other entries are zeros. 7 > > 7 > = ) = 6 0. 2) its supradiagonal entries are either zeros or ones; Web first nd all the eigenvectors of t corresponding to a certain eigenvalue! Web jordan normal form chapter 8 jordan normal form 8.1 minimal polynomials recall pa(x)=det(xi −a) is called the characteristic polynomial of.
Calculating the Jordan form of a matrix SciPy Recipes
Web a matrix is said to be in jordan form if 1) its diagonal entries are equal to its eigenvalues; Mathematica by example (fifth edition), 2017. Web because the jordan form of a numeric matrix is sensitive to numerical errors, first convert the matrix to symbolic form by using sym. How to use jordan normal forms to compute something with.
Jordan form of a matrix Cheenta
Web i've seen from many sources that if given a matrix j (specifically 3x3) that is our jordan normal form, and we have our matrix a, then there is some p such that. 7 > > 7 > = ) = 6 0. 3) all its other entries are zeros. Such a matrix ai is called a jordan block corresponding.
Find the Jordan form and a modal matrix for the
We also say that the. Such a matrix ai is called a jordan block corresponding to , and the matrix [t ] is called a jordan form of t. Web jordan forms lecture notes for ma1212 p. Eigenvectors you found gives you the number of jordan blocks (here there was only. Web i've seen from many sources that if given.
Overview of Jordan Canonical Form YouTube
How to use jordan normal forms to compute something with matrices? 3) all its other entries are zeros. Web jordan normal form chapter 8 jordan normal form 8.1 minimal polynomials recall pa(x)=det(xi −a) is called the characteristic polynomial of the matrix a. Web a matrix is said to be in jordan form if 1) its diagonal entries are equal to.
Jordan Canonical Form of a Matrix Linear Algebra YouTube
Web the jordan form of a matrix is not uniquely determined, but only up to the order of the jordan blocks. Find the jordan form j and the matrix m for a and b (b has eigenvalues 1, 1, 1, −1). We also say that the. Mathematica by example (fifth edition), 2017. 3) all its other entries are zeros.
Web For The Matrix , Interpret The Columns Of The Matrix Of The Jordan Decomposition In Terms Of True Eigenvectors And Generalized Eigenvectors:
Web i've seen from many sources that if given a matrix j (specifically 3x3) that is our jordan normal form, and we have our matrix a, then there is some p such that. Web a matrix is said to be in jordan form if 1) its diagonal entries are equal to its eigenvalues; Web first nd all the eigenvectors of t corresponding to a certain eigenvalue! We also say that the.
7 > > 7 > = ) = 6 0.
The jordan matrix corresponds to the second element of ja extracted with ja[[2]] and displayed in matrixform. Web they cover definitions, examples and first properties for invariant subspaces, jordan form for invariant subspaces, coinvariant and semiinvariant subspaces, jordan form for. More exactly, two jordan matrices are similar over $ a $ if. Eigenvectors you found gives you the number of jordan blocks (here there was only.
C C @ 1 A For Some Eigenvalue Of T.
How to use jordan normal forms to compute something with matrices? Mathematica by example (fifth edition), 2017. 2) its supradiagonal entries are either zeros or ones; Such a matrix ai is called a jordan block corresponding to , and the matrix [t ] is called a jordan form of t.
3) All Its Other Entries Are Zeros.
Web because the jordan form of a numeric matrix is sensitive to numerical errors, first convert the matrix to symbolic form by using sym. Web jordan normal form chapter 8 jordan normal form 8.1 minimal polynomials recall pa(x)=det(xi −a) is called the characteristic polynomial of the matrix a. Web jordan forms lecture notes for ma1212 p. A jordan block is a matrix of the form j1( ) = 2 c when k = 1 and jk( 2 1 6 0 6 6 0 0 0 3 9.