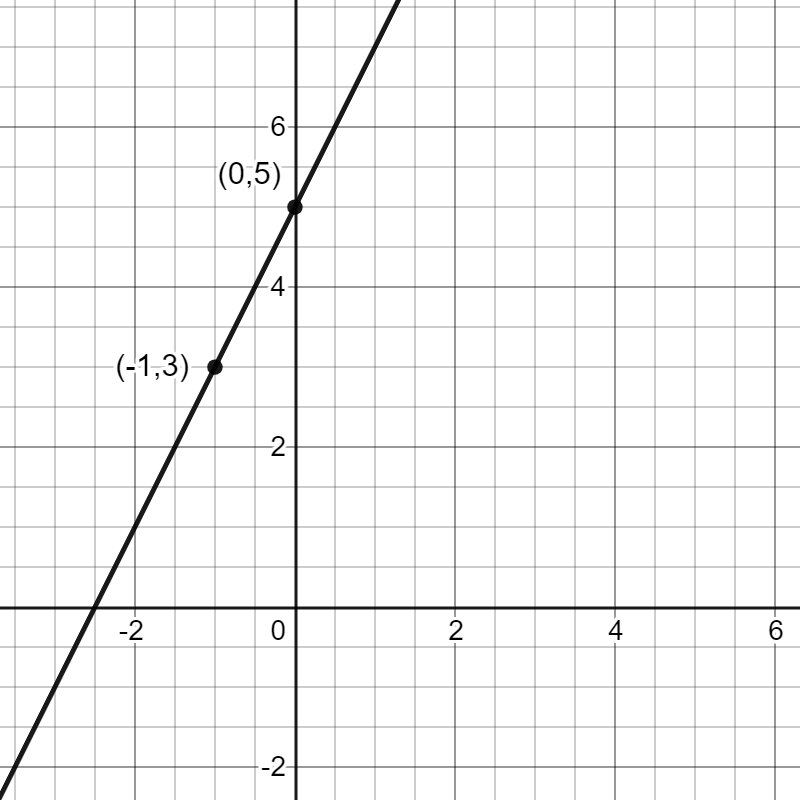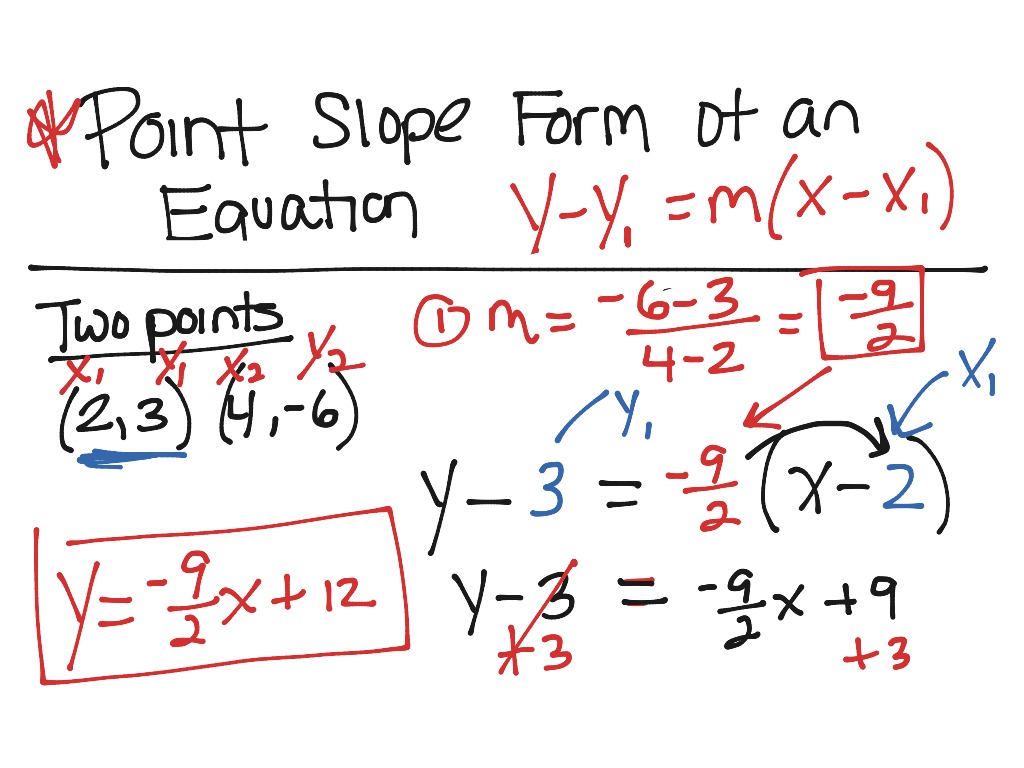Definition Of Point Slope Form In Math
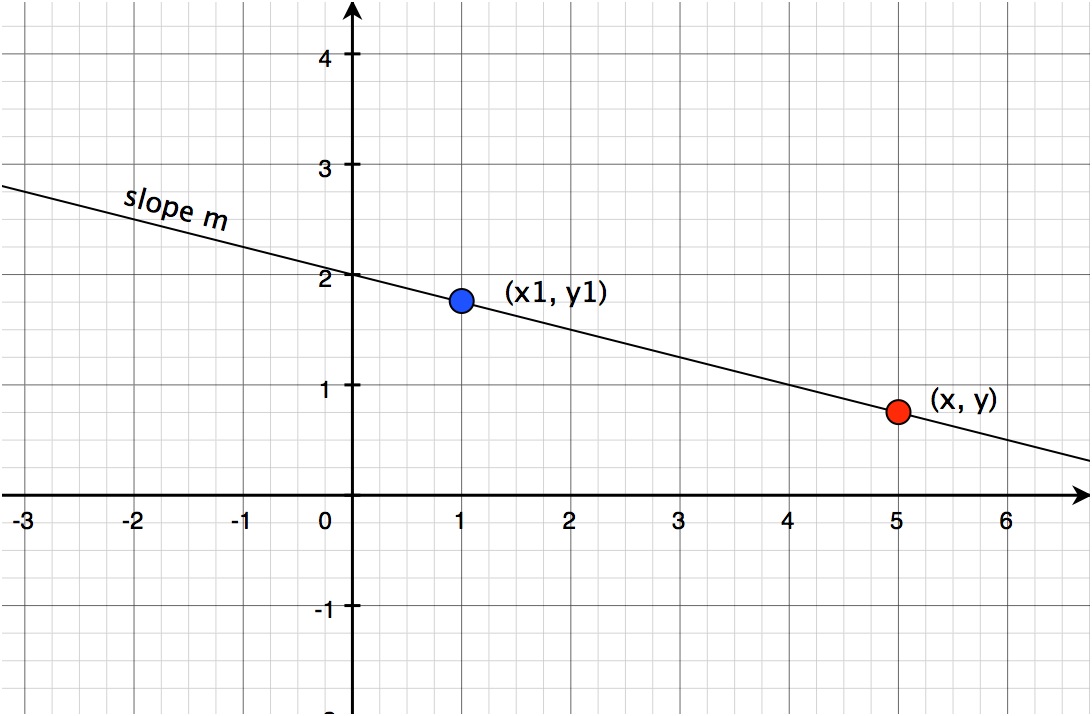
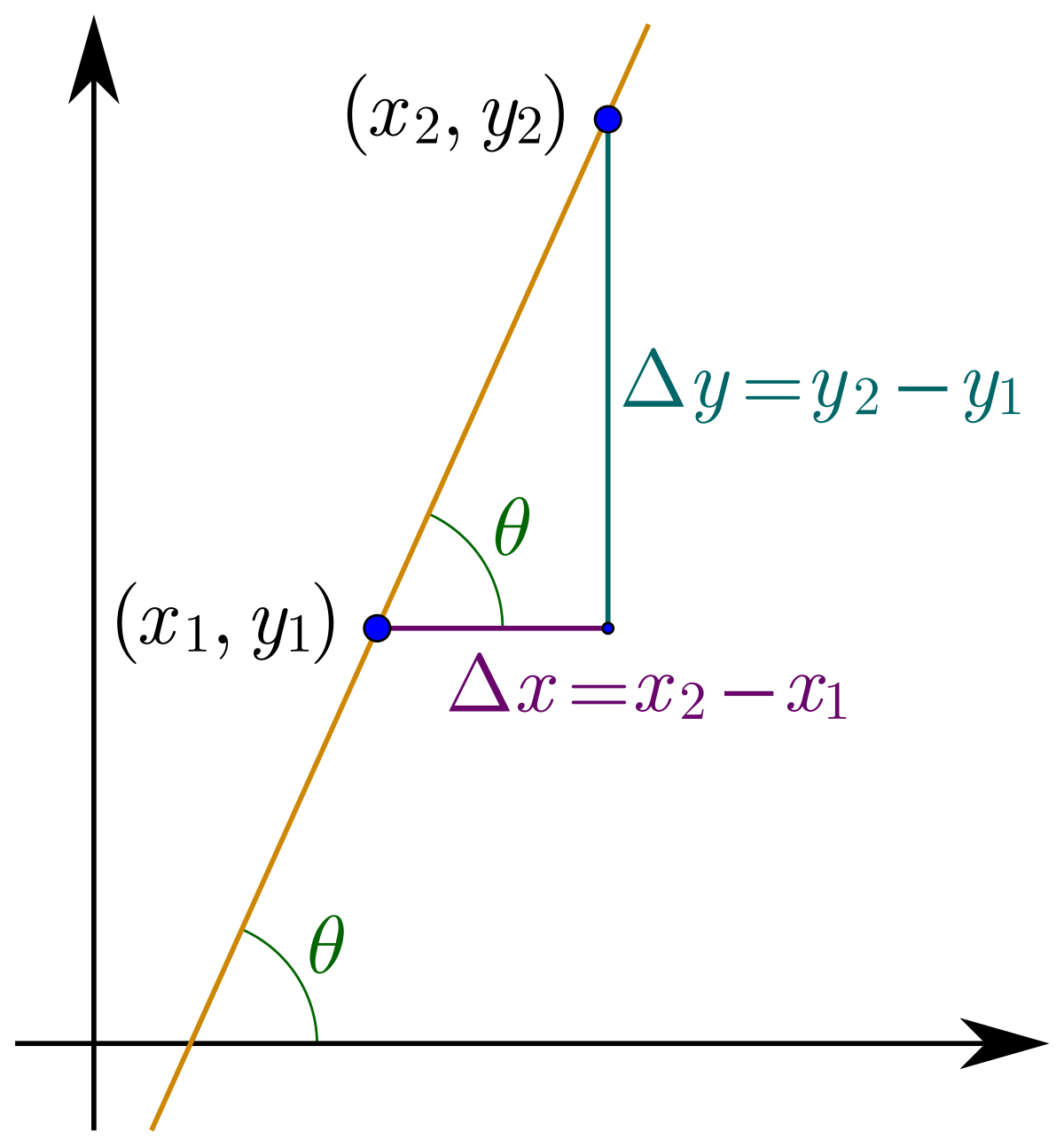
Definition Of Point Slope Form In Math - As the name suggests, linear. If a line is vertical the slope is undefined (see below). The point form is written as (x,y) and the. The net change in y coordinate is δy, while the net change in the. Y − y 1 = m (x − x 1) the equation is useful when we know: Physically, it represents the steepness of the line joining the. (x1, y1) and the slope of the. If a line is horizontal the slope is zero. One point on the line: Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line.
The point form is written as (x,y) and the. (x1, y1) and the slope of the. As the name suggests, linear. If a line is horizontal the slope is zero. Web the point slope form of a linear equation is either summation, difference, multiplication, or combination of all, variables and numbers. The rise of a road between two points is the difference. Physically, it represents the steepness of the line joining the. One point on the line: Web we now draw a line through the point p(−2, 2) that is parallel to the line through the points q and r. If a line is vertical the slope is undefined (see below).
Web the point slope form of a linear equation is either summation, difference, multiplication, or combination of all, variables and numbers. One point on the line: Web we now draw a line through the point p(−2, 2) that is parallel to the line through the points q and r. Y − y 1 = m (x − x 1) the equation is useful when we know: If a line is vertical the slope is undefined (see below). Physically, it represents the steepness of the line joining the. As the name suggests, linear. The point form is written as (x,y) and the. Arranging equations in a particular format gives us insight. Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line.
Point Slope Form Rules The Reasons Why We Love Point Slope Form Rules
Parallel lines must have the same slope, so we start at the point p(−2, 2),. Web we now draw a line through the point p(−2, 2) that is parallel to the line through the points q and r. One point on the line: Arranging equations in a particular format gives us insight. As the name suggests, linear.
point slope form 수학
This is a constant function. Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line. Arranging equations in a particular format gives us insight. Web the point slope form of a linear equation is either summation, difference, multiplication, or combination of all, variables and numbers..
Point Slope Form
(x1, y1) and the slope of the. Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line. Y − y 1 = m (x − x 1) the equation is useful when we know: The point form is written as (x,y) and the. Web the.
Slope Wikipedia
As the name suggests, linear. Physically, it represents the steepness of the line joining the. Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line. The point form is written as (x,y) and the. Arranging equations in a particular format gives us insight.
Point Slope Format amulette
The net change in y coordinate is δy, while the net change in the. As the name suggests, linear. This is a constant function. Arranging equations in a particular format gives us insight. Y − y 1 = m (x − x 1) the equation is useful when we know:
Find The Slope Of A Line Whose Equation Is 4y 3x 8 Tessshebaylo
The point form is written as (x,y) and the. (x1, y1) and the slope of the. Web the slope (or gradient) is defined as the ratio of the difference between two points’ vertical and horizontal coordinates. If a line is horizontal the slope is zero. Web we now draw a line through the point p(−2, 2) that is parallel to.
Understanding Point Slope Form Math Concepts Explained
Parallel lines must have the same slope, so we start at the point p(−2, 2),. Physically, it represents the steepness of the line joining the. As the name suggests, linear. If a line is horizontal the slope is zero. If a line is vertical the slope is undefined (see below).
PointSlope Form Explanation, Review, and Examples Albert Resources
Web the slope (or gradient) is defined as the ratio of the difference between two points’ vertical and horizontal coordinates. The point form is written as (x,y) and the. Arranging equations in a particular format gives us insight. (x1, y1) and the slope of the. Parallel lines must have the same slope, so we start at the point p(−2, 2),.
Point slope form of a line Math, Algebra ShowMe
Web the slope (or gradient) is defined as the ratio of the difference between two points’ vertical and horizontal coordinates. Y − y 1 = m (x − x 1) the equation is useful when we know: One point on the line: This is a constant function. The point form is written as (x,y) and the.
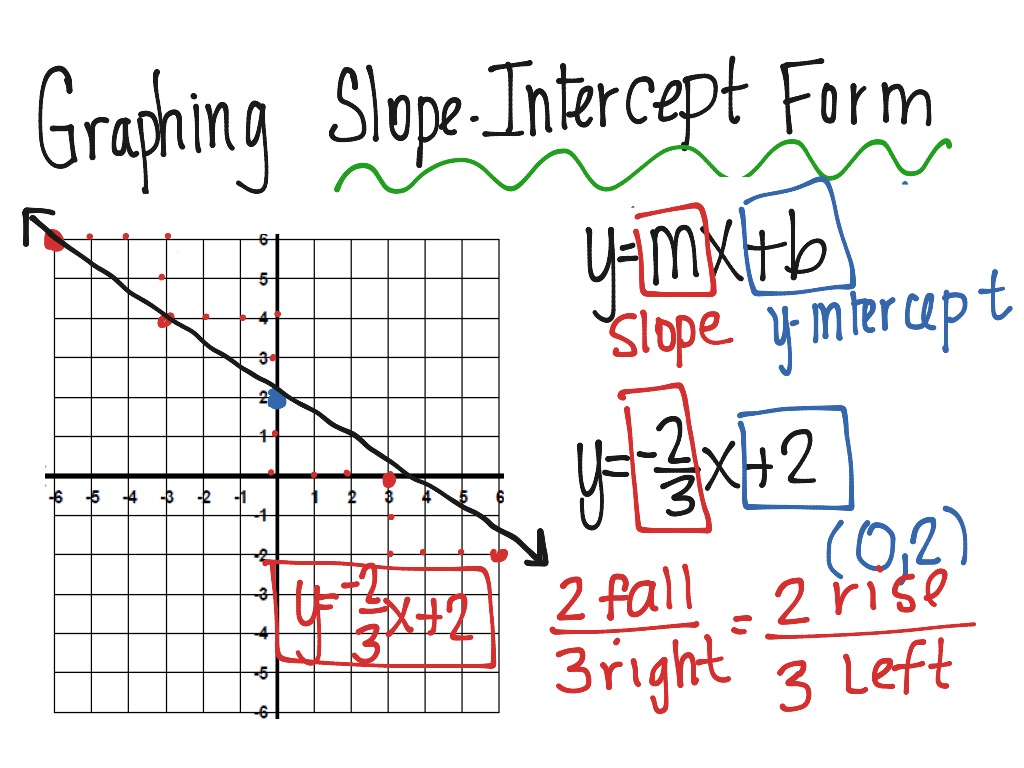
Graphing Slope Intercept Form Math ShowMe
This is a constant function. Parallel lines must have the same slope, so we start at the point p(−2, 2),. Arranging equations in a particular format gives us insight. As the name suggests, linear. Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line.
Web We Now Draw A Line Through The Point P(−2, 2) That Is Parallel To The Line Through The Points Q And R.
(x1, y1) and the slope of the. If a line is vertical the slope is undefined (see below). This is a constant function. As the name suggests, linear.
If A Line Is Horizontal The Slope Is Zero.
The point form is written as (x,y) and the. Arranging equations in a particular format gives us insight. Web the point slope form of a linear equation is either summation, difference, multiplication, or combination of all, variables and numbers. Web the slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line.
One Point On The Line:
Parallel lines must have the same slope, so we start at the point p(−2, 2),. Web the slope (or gradient) is defined as the ratio of the difference between two points’ vertical and horizontal coordinates. Physically, it represents the steepness of the line joining the. The rise of a road between two points is the difference.
Y − Y 1 = M (X − X 1) The Equation Is Useful When We Know:
The net change in y coordinate is δy, while the net change in the.
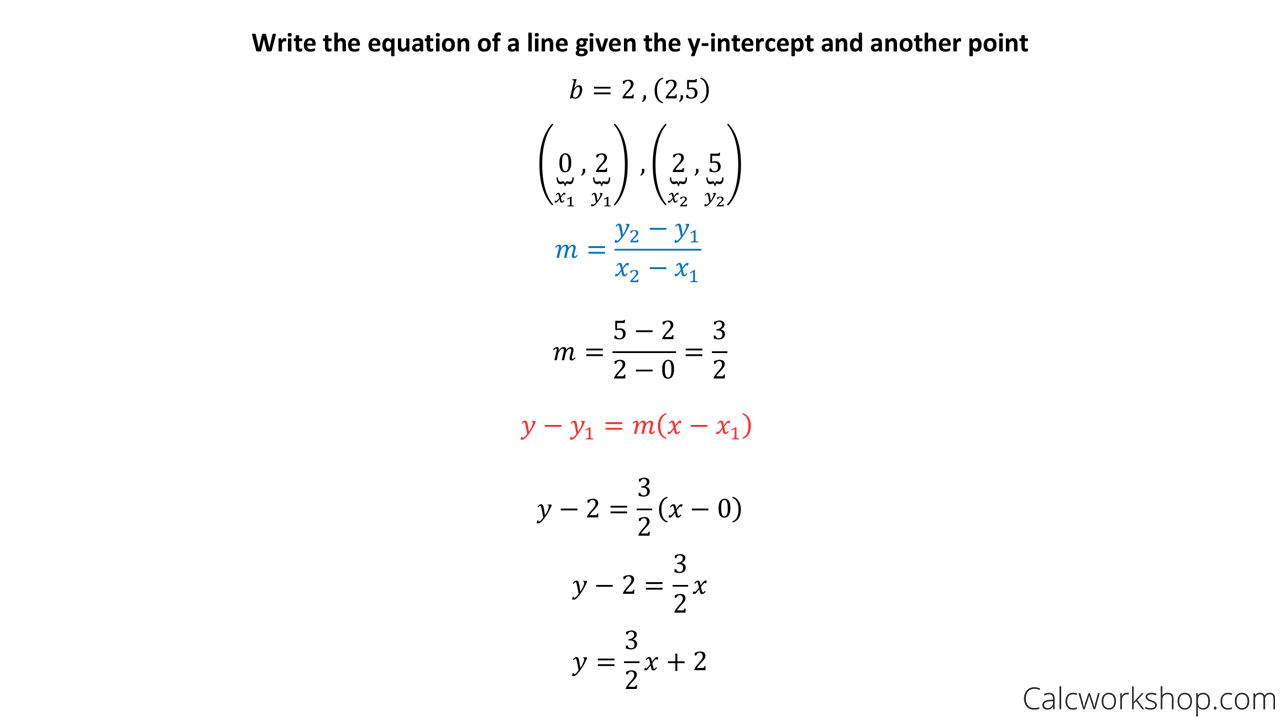



-Step-24-Version-2.jpg)